solution

We now wish to illustrate how several op amp circuits can be interconnected to solve a differential equation.

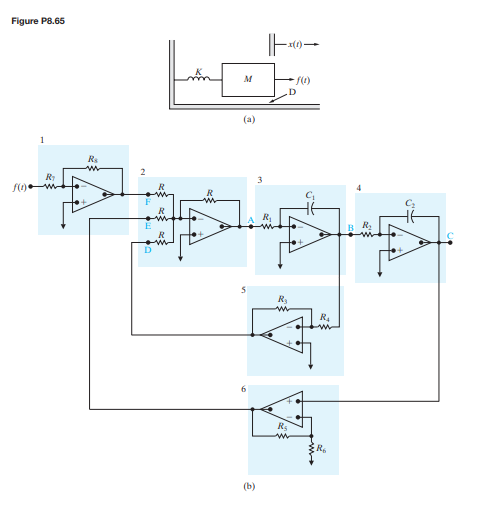
 a) Derive the differential equation for the springmass system shown in Fig. P8.65(a). Assume that the force exerted by the spring is directly proportional to the spring displacement, that the mass is constant, and that the frictional force is directly proportional to the velocity of the moving mass.

 b) Rewrite the differential equation derived in (a) so that the highest order derivative is expressed as a function of all the other terms in the equation. Now assume that a voltage equal to d2 x>dt2 is available and by successive integrations generates dx>dt and x. We can synthesize the coefficients in the equations by scaling amplifiers, and we use a summing amplifier to combine the terms required to generate d² x/dt² . With these ideas in mind, analyze the interconnection shown in Fig. P8.65(b). In particular, describe the purpose of each shaded area in the circuit and describe the signal at the points labeled B, C, D, E, and F, assuming the signal at A represents d² x/dt² . Also discuss the parameters R; R₁, C₁; R₂, C₂; R₃, R₄; R₅, R₆; and R₇, R₈ in terms of the coefficients in the differential equation.