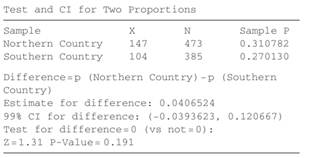
dolution
dolution.
pH in Rain An environmentalist wanted to determine if the mean acidity of rain differed among Alaska, Florida, and Texas. He randomly selected six rain dates at each of the three locations and obtained the following data:
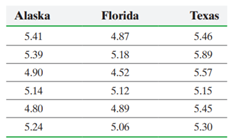
(a) State the null and alternative hypotheses.
(b) Verify that the requirements to use the one-way ANOVA procedure are satisfied. Normal probability plots indicate that the sample data come from a normal population.
(c) Test the hypothesis that the mean pHs in the rainwater are the same at the ![]() ÃÂ level of significance.
ÃÂ level of significance.
(d) Draw boxplots of the pH in rain for the three states to support the results obtained in part (c).
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"